TRANSFORMADA DE LAPLACE

DEFINICION

La transformada de Laplace es un operador LINEAL muy útil para la resolución de ecuaciones diferenciales.

La Transformada de Laplace es una técnica Matemática que forma parte de ciertas transformadas integrales como la transformada de Fourier, la transformada de Hilbert, y la transformada de Mellin entre otras.

Estas transformadas están definidas por medio de una integral impropia y cambian una función en una variable de entrada en otra función en otra variable. La transformada de Laplace puede ser usada para resolver Ecuaciones Diferenciales Lineales y Ecuaciones Integrales. Aunque se pueden resolver algún tipo de ED con coeficientes variables, en general se aplica a problemas con coeficientes constantes. Un requisito adicional es el conocimiento de las condiciones iniciales a la misma ED. Su mayor ventaja sale a relucir cuando la función en la variable independiente que aparece en la ED es una función seccionada.

MODELO MATEMÁTICO

En estos casos el problema se plantea en términos de una segunda variable que permite resolver el problema en forma algebraica. Luego de hallada esta solución, regresando a la variable original se obtiene la solución de la ecuación diferencial planteada. La limitación de este procedimiento es que sólo puede ser aplicado en ecuaciones diferenciales lineales.

La ecuación general es: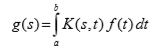

g(s)= función transformada

K(s,t)= núcleo de la transformación

Para las transformadas de Laplace se cumple que: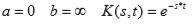

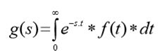
La transformada de Laplace es un método operacional que se usa para resolver ecuaciones diferenciales lineales en los problemas de dinámica de control.

Existencia de la Transformada

Condiciones suficientes para la existencia de la transformada de Laplace para  de una función cualquiera:

Estar definida y ser continua a pedazos en el intervalo 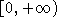 Ser de orden exponencial  

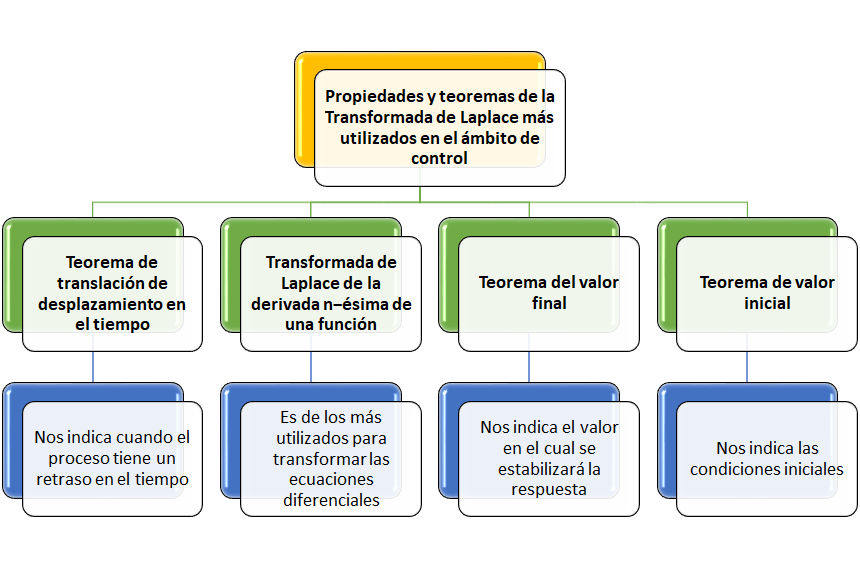
PROPIEDADES

APLICACIONES PARA EL CONTROL Y LA INSTRUMENTACIÓN

• El campo de aplicación de los sistemas de control es muy amplia. Y una herramienta que se utiliza en el diseño de control clásico es La transformada de Laplace.
• En el estudio de los procesos es necesario considerar modelos dinámicos, es decir, modelos de comportamiento variable respecto al tiempo. Esto trae como consecuencia el uso de ecuaciones diferenciales respecto al tiempo para representar matemáticamente el comportamiento de un proceso.
• La transformada de Laplace es una herramienta matemática muy útil para el análisis de sistemas dinámicos lineales. De hecho, la transformada de Laplace permite resolver ecuaciones diferenciales lineales. Lo que hace es plantear el problema en términos de una segunda variable que permite resolver el problema en forma algebraica con lo cual se facilita su estudio. Luego de hallada esta solución, regresando a la variable original se obtiene la solución de la ecuación diferencial planteada.
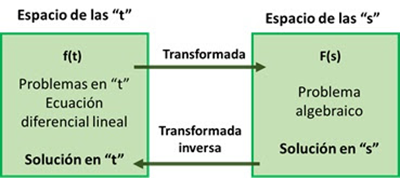
• Una vez que se ha estudiado el comportamiento de los sistemas dinámicos, se puede proceder a diseñar y analizar los sistemas de control de manera simple
• En instrumentación, la ventaja de trabajar con las transformaciones de Laplace es que existen tablas de conversión muy extensas que cubren prácticamente la totalidad de las funciones que puedan surgir al analizar los sistemas controlados.

CASO PRÁCTICO EN LA INDUSTRIA

Intercambiador de Calor

Se tiene un intercambiador de calor 1-1, de tubos y coraza. En condiciones estables, este intercambiador calienta 224 gal/min de agua de 80°F a 185°F por dentro de tubos mediante un vapor saturado a 150 psia.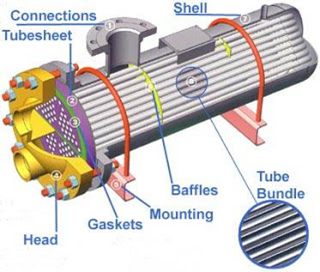

En un instante dado, la temperatura del vapor y el flujo de agua cambian, produciéndose una perturbación en el intercambiador.

a) Obtenga la función de transferencia del cambio de la temperatura de salida del agua con respecto a un cambio en la temperatura del vapor y un cambio en el flujo de agua, suponiendo que la temperatura de entrada del agua al intercambiador se mantiene constante en 80°F.

b) Determine el valor final de la temperatura de salida del agua ante un cambio tipo escalón de +20°F en la temperatura del vapor, y un cambio de +10 gal/min en el flujo de agua.

Ecuacion Diferencial: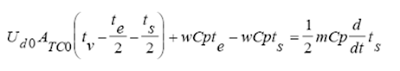

Donde:

Linealizando

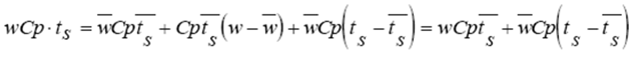
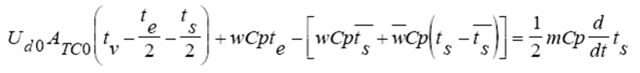Evaluando en condiciones iniciales estables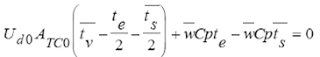Restando (2) de (3)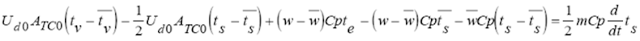Utilizando variables de desviación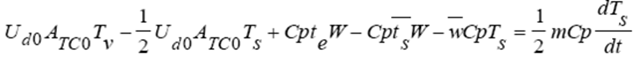Aplicando la transformada con Laplace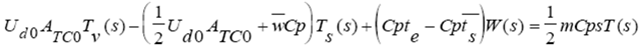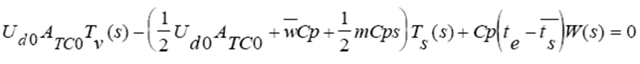Simplificando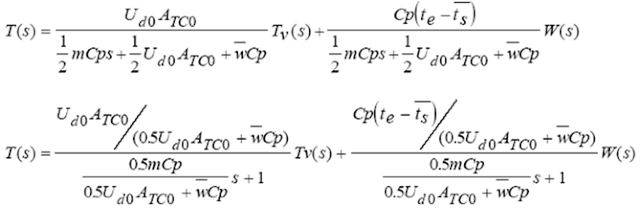

Datos físicos

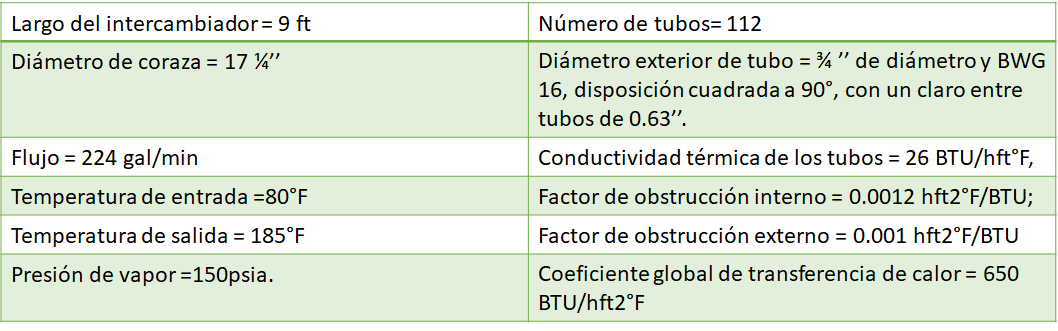
Calculando las constantesFunción de transferencia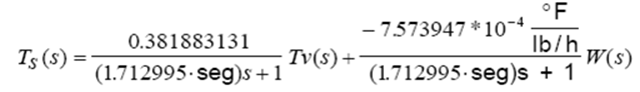Determine el valor final de la temperatura de salida del agua ante un cambio tipo escalón de +20°F en la temperatura del vapor, y un cambio de +10 gal/min en el flujo de agua.